DIP-Concept of Convolution
This tutorial is about one of the very important concept of signals and system. We will completely discuss convolution. What is it? Why is it? What can we achieve with it?
We will start discussing convolution from the basics of image processing.
What is image processing
As we have discussed in the introduction to image processing tutorials and in the signal and system that image processing is more or less the study of signals and systems because an image is nothing but a two dimensional signal.
Also we have discussed, that in image processing , we are developing a system whose input is an image and output would be an image. This is pictorially represented as.
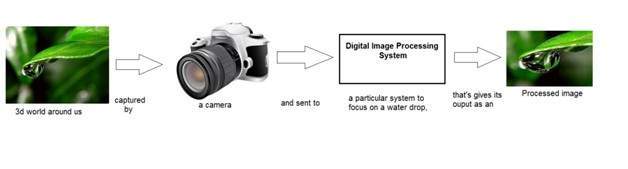
The box is that is shown in the above figure labeled as “Digital Image Processing system” could be thought of as a black box
It can be better represented as:

Where have we reached until now
Till now we have discussed two important methods to manipulate images. Or in other words we can say that, our black box works in two different ways till now.
The two different ways of manipulating images were
Graphs (Histograms)

This method is known as histogram processing. We have discussed it in detail in previous tutorials for increase contrast, image enhancement, brightness e.t.c
Transformation functions
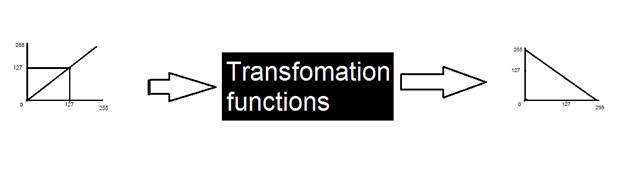
This method is known as transformations, in which we discussed different type of transformations and some gray level transformations
Another way of dealing images
Here we are going to discuss another method of dealing with images. This other method is known as convolution. Usually the black box(system) used for image processing is an LTI system or linear time invariant system. By linear we mean that such a system where output is always linear , neither log nor exponent or any other. And by time invariant we means that a system which remains same during time.
So now we are going to use this third method. It can be represented as.

It can be mathematically represented as two ways
g(x,y) = h(x,y) * f(x,y)
It can be explained as the “mask convolved with an image”.
Or
g(x,y) = f(x,y) * h(x,y)
It can be explained as “image convolved with mask”.
There are two ways to represent this because the convolution operator(*) is commutative. The h(x,y) is the mask or filter.
What is mask?
Mask is also a signal. It can be represented by a two dimensional matrix. The mask is usually of the order of 1x1, 3x3, 5x5, 7x7 . A mask should always be in odd number, because other wise you cannot find the mid of the mask. Why do we need to find the mid of the mask. The answer lies below, in topic of, how to perform convolution?
How to perform convolution?
In order to perform convolution on an image, following steps should be taken.
- Flip the mask (horizontally and vertically) only once
- Slide the mask onto the image.
- Multiply the corresponding elements and then add them
- Repeat this procedure until all values of the image has been calculated.
Example of convolution
Let’s perform some convolution. Step 1 is to flip the mask.
Mask
Let’s take our mask to be this.
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
Flipping the mask horizontally
| 3 | 2 | 1 |
| 6 | 5 | 4 |
| 9 | 8 | 7 |
Flipping the mask vertically
| 9 | 8 | 7 |
| 6 | 5 | 4 |
| 3 | 2 | 1 |
Image
Let’s consider an image to be like this
| 2 | 4 | 6 |
| 8 | 10 | 12 |
| 14 | 16 | 18 |
Convolution
Convolving mask over image. It is done in this way. Place the center of the mask at each element of an image. Multiply the corresponding elements and then add them , and paste the result onto the element of the image on which you place the center of mask.
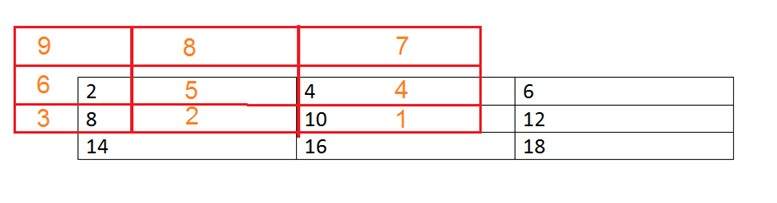
The box in red color is the mask, and the values in the orange are the values of the mask. The black color box and values belong to the image. Now for the first pixel of the image, the value will be calculated as
First pixel = (5*2) + (4*4) + (2*8) + (1*10)
= 10 + 16 + 16 + 10
= 52
Place 52 in the original image at the first index and repeat this procedure for each pixel of the image.
Why Convolution
Convolution can achieve something, that the previous two methods of manipulating images can’t achieve. Those include the blurring, sharpening, edge detection, noise reduction e.t.c.