High Pass vs Low Pass Filters
In the last tutorial, we briefly discuss about filters. In this tutorial we will thoroughly discuss about them. Before discussing about let’s talk about masks first. The concept of mask has been discussed in our tutorial of convolution and masks.
Blurring masks vs derivative masks
We are going to perform a comparison between blurring masks and derivative masks.
Blurring masks
A blurring mask has the following properties.
- All the values in blurring masks are positive
- The sum of all the values is equal to 1
- The edge content is reduced by using a blurring mask
- As the size of the mask grow, more smoothing effect will take place
Derivative masks
A derivative mask has the following properties.
- A derivative mask have positive and as well as negative values
- The sum of all the values in a derivative mask is equal to zero
- The edge content is increased by a derivative mask
- As the size of the mask grows , more edge content is increased
Relationship between blurring mask and derivative mask with high pass filters and low pass filters.
The relationship between blurring mask and derivative mask with a high pass filter and low pass filter can be defined simply as.
- Blurring masks are also called as low pass filter
- Derivative masks are also called as high pass filter
High pass frequency components and Low pass frequency components
The high pass frequency components denotes edges whereas the low pass frequency components denotes smooth regions.
Ideal low pass and Ideal High pass filters
This is the common example of low pass filter.
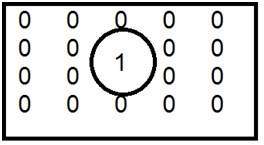
When one is placed inside and the zero is placed outside , we got a blurred image. Now as we increase the size of 1, blurring would be increased and the edge content would be reduced.
This is a common example of high pass filter.
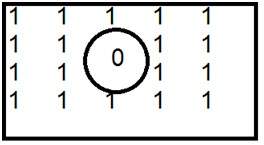
When 0 is placed inside, we get edges, which gives us a sketched image. An ideal low pass filter in frequency domain is given below.

The ideal low pass filter can be graphically represented as
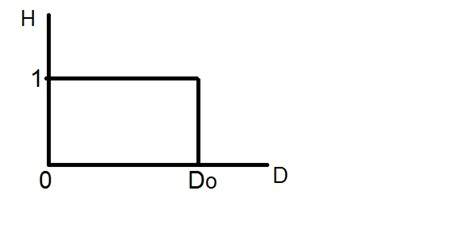
Now let’s apply this filter to an actual image and let’s see what we got.
Sample image

Image in frequency domain

Applying filter over this image

Resultant Image

With the same way, an ideal high pass filter can be applied on an image. But obviously the results would be different as, the low pass reduces the edged content and the high pass increase it.
Gaussian Low pass and Gaussian High pass filter
Gaussian low pass and Gaussian high pass filter minimize the problem that occur in ideal low pass and high pass filter.
This problem is known as ringing effect. This is due to reason because at some points transition between one color to the other cannot be defined precisely, due to which the ringing effect appears at that point.
Have a look at this graph.
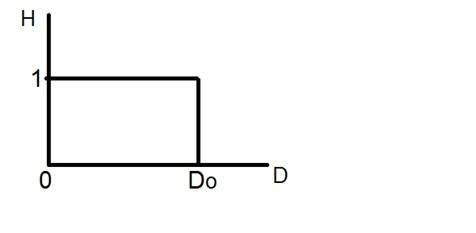
This is the representation of ideal low pass filter. Now at the exact point of Do, you cannot tell that the value would be 0 or 1. Due to which the ringing effect appears at that point.
So in order to reduce the effect that appears is ideal low pass and ideal high pass filter, the following Gaussian low pass filter and Gaussian high pass filter is introduced.
Gaussian Low pass filter
The concept of filtering and low pass remains the same, but only the transition becomes different and become more smooth.
The Gaussian low pass filter can be represented as
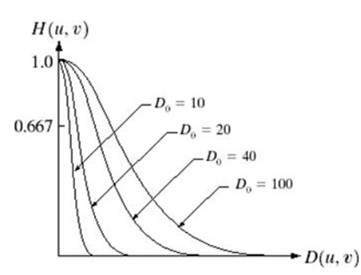
Note the smooth curve transition, due to which at each point, the value of Do, can be exactly defined.
Gaussian high pass filter
Gaussian high pass filter has the same concept as ideal high pass filter, but again the transition is more smooth as compared to the ideal one.